/ The Montessori Method - R... / German

Created by Montessori X, last update Aug 10, 2022 (History)

Kapitel 19 - Zahlenlehre: Einführung in die Arithmetik

Die Montessori-Methode, 2. Auflage - Wiederherstellung

Table of Contents

Kapitel 19 - Zahlenlehre, Einführung in die Arithmetik

Kinder von drei Jahren können bereits beim Eintritt in unsere Schulen bis zwei oder drei zählen. Sie lernen daher sehr leicht das Zählen, das darin besteht, Gegenstände zu zählen . Ein Dutzend verschiedener Wege kann diesem Ziel dienen, und das tägliche Leben bietet viele Gelegenheiten; wenn die Mutter zum Beispiel sagt: „An deiner Schürze fehlen zwei Knöpfe“ oder „Wir brauchen noch drei Teller am Tisch“.

Eines der ersten von mir angewandten Mittel ist das Zählen mit Geld. Ich verdiene neues Geld, und wenn es möglich wäre, würde ich gute Reproduktionen aus Karton machen lassen. Ich habe gesehen, wie solches Geld in einer Schule für Mangelhafte in London verwendet wurde.

Das Ändern ist eine Form der Zählung, die so attraktiv ist, dass sie die Aufmerksamkeit des Kindes auf sich zieht. Ich präsentiere die Ein-, Zwei- und Vierrappenstücke, und die Kinder lernen so, bis zehn zu zählen .

Keine Form des Unterrichts ist praktischer als die, Kinder mit den gebräuchlichen Münzen vertraut zu machen, und keine Übung ist nützlicher als das Wechselgeld. Es ist so eng mit dem täglichen Leben verbunden, dass es alle Kinder sehr interessiert.

Nachdem ich das Numerieren in dieser empirischen Weise gelehrt habe, gehe ich zu methodischeren Übungen über, wobei ich als didaktisches Material einen der Sätze von Blöcken habe, die bereits in der Sinneserziehung verwendet werden; nämlich die Reihe von zehn Stäben, die bisher zum Lehren der Länge verwendet wurden. Der kürzeste dieser Stäbe entspricht einem Dezimeter, der längste einem Meter, während die dazwischen liegenden Stäbe in Abschnitte mit einer Länge von einem Dezimeter unterteilt sind. Die Abschnitte sind abwechselnd rot und blau bemalt.

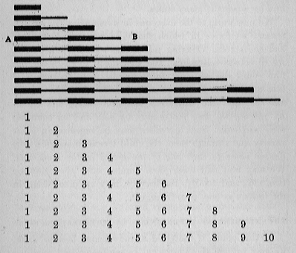
Eines Tages, wenn ein Kind die Stäbe der Länge nach geordnet hat, lassen wir es die roten und blauen Zeichen zählen, beginnend mit dem kleinsten Stück; das heißt, eins; eins zwei; eins, zwei, drei usw., wobei er beim Zählen jedes Stabes immer auf eins zurückgeht und von der Seite A ausgeht. Wir lassen ihn dann die einzelnen Stäbe vom kürzesten bis zum längsten nach der Gesamtzahl der Abschnitte benennen die jeweils enthält, berühren die Stäbe an der Seite B, auf welcher Seite die Treppe aufsteigt. Dies ergibt die gleiche Nummerierung wie beim Zählen der längsten Stange 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Um die Anzahl der Stangen zu wissen, zählen wir sie von Seite A und gleich Nummerierungsergebnisse; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Wir vereinen nun die Übungen im Zählen mit den früheren sensorischen Übungen, bei denen das Kind die langen und kurzen Stäbchen erkannt hat. Nachdem sie die Stangen auf einen Teppich gemischt hat, wählt die Direktorin eine aus, zeigt sie dem Kind und lässt es die Abschnitte zählen; zum Beispiel 5. Sie bittet ihn dann, ihr die nächste Länge zu geben. Er wählt es nach seinem Auge aus, und die Direktorin lässt ihn seine Wahl bestätigen, indem sie die beiden Teile nebeneinander legt und ihre Abschnitte zählt . Solche Übungen können vielfältig wiederholt werden und das Kind lernt dadurch, jedem der Teile der langen Treppe einen bestimmten Namen zuzuordnen . Wir können sie jetzt Stück Nummer eins nennen; Stück Nummer zwei usw., und schließlich kann man sie der Kürze halber in den Lektionen als eins, zwei, drei usw. bezeichnen.

19.1 Zahlen, dargestellt durch grafische Zeichen

Wenn das Kind bereits schreiben kann, können wir an dieser Stelle die in Sandpapier geschnittenen und auf Karten montierten Figuren präsentieren. Beim Präsentieren dieser ist die Methode dieselbe, die beim Lehren der Buchstaben verwendet wird. "Dies ist einer." "Das ist zwei." "Gib mir eins." "Gib mir zwei." "Welche Nummer ist das?" Das Kind fährt mit dem Finger die Zahl nach wie die Buchstaben.

Übungen mit Zahlen . Zuordnung des grafischen Zeichens zur Menge.

Ich habe zwei Tabletts entworfen, die jeweils in fünf kleine Fächer unterteilt sind. Auf der Rückseite jedes Fachs kann eine Karte mit einer Figur platziert werden. Die Zahlen im ersten Fach sollten 0, 1, 2, 3, 4 und im zweiten 5, 6, 7, 8 und 9 sein.

Die Übung ist offensichtlich; es besteht darin, in die Fächer einige Gegenstände zu legen, die der Zahl entsprechen, die auf der Karte auf der Rückseite des Fachs angegeben ist. Wir geben den Kindern verschiedene Gegenstände, um den Unterricht zu variieren, verwenden aber hauptsächlich große Holzstifte, die so geformt sind, dass sie nicht vom Tisch rollen. Wir legen eine Anzahl davon vor das Kind, dessen Aufgabe es ist, sie an ihren Platz zu bringen, einen Stift, der der mit einem markierten Karte entspricht usw. Wenn es fertig ist, bringt es sein Tablett zur Direktorin, damit sie seine Arbeit überprüfen kann.

Die Lektion über Null . Wir warten, bis das Kind, auf das Fach mit der Karte mit der Null zeigend, fragt: „Und was muss ich hier reinstecken?“ Wir antworten dann: "Nichts; Null ist nichts." Aber oft reicht das nicht aus. Es ist notwendig, das Kind fühlen zu lassen, was wir mit nichts meinen . Dazu nutzen wir kleine Spiele, die die Kinder mächtig unterhalten. Ich stehe zwischen ihnen und wende mich an einen von ihnen, der dieses Material bereits verwendet hat, und sage: "Komm, Liebes, komm null Mal zu mir." Das Kind kommt fast immer zu mir und rennt dann zu seinem Platz zurück. „Aber mein Junge, du bist einmal gekommen , und ich habe dir gesagt , du sollst Null kommen Mal.“ Dann beginnt er sich zu fragen. „Aber was muss ich dann tun?“ „Nichts; Null ist nichts.“ „Aber wie soll ich nichts tun?“ „Nichts tun. Du musst stillsitzen. Du darfst überhaupt nicht kommen, zu keiner Zeit. Nullmal. Gar keine Zeit.“ Diese Übungen wiederhole ich so lange, bis die Kinder es verstehen, und sie amüsieren sich dann ungemein darüber, ruhig zu bleiben, wenn ich sie aufrufe, null Mal zu mir zu kommen oder mir null Küsse zuzuwerfen. Oft schreien sie: „Null ist nichts! Null ist nichts!"

19.2 Übungen zum Zahlengedächtnis

Wenn die Kinder die geschriebene Zahl erkennen und diese Zahl ihnen den Zahlenwert bedeutet, gebe ich ihnen folgende Übung:

Ich schneide die Figuren aus alten Kalendern aus und klebe sie auf Zettel, die dann gefaltet und in eine Schachtel geworfen werden. Die Kinder ziehen die Zettel heraus und tragen sie noch zusammengefaltet zu ihren Plätzen, wo sie sie betrachten und neu zusammenfalten, um das Geheimnis zu bewahren . Dann gehen diese Kinder (natürlich die Ältesten in der Klasse) einzeln oder in Gruppen zum großen Tisch der Direktorin, wo Gruppen von verschiedenen kleinen Gegenständen stehen. Jeder wählt die Menge an Gegenständen aus, die der von ihm gezogenen Zahl entspricht. Die Nummer wurde unterdessen beim Kind hinterlassen , ein geheimnisvoll gefalteter Zettel. Das Kind muss sich also erinnern seine Zahl nicht nur während der Bewegungen, die er beim Kommen und Gehen macht, sondern während er seine Stücke sammelt und sie einzeln zählt. Die Direktorin mag hier interessante Einzelbeobachtungen zum Zahlengedächtnis machen.

Wenn das Kind seine Gegenstände eingesammelt hat, ordnet es sie auf seinem eigenen Tisch an, in Zweierspalten, und wenn die Anzahl ungerade ist, legt es das ungerade Stück unten und zwischen die letzten beiden Gegenstände. Die Anordnung der Stücke ist daher wie folgt:

o	o	o	o	o	o	o	o	o	o
X	XX	XX	XX	XX	XX	XX	XX	XX	XX
 		X	XX	XX	XX	XX	XX	XX	XX
 				X	XX	XX	XX	XX	XX
 						X	XX	XX	XX
 								X	XX

Die Kreuze stellen die Gegenstände dar, während der Kreis für den gefalteten Zettel mit der Figur steht. Nachdem es seine Gegenstände arrangiert hat, wartet das Kind auf die Überprüfung. Die Direktorin kommt, öffnet den Zettel, liest die Nummer und zählt die Stücke.

Als wir dieses Spiel zum ersten Mal spielten, kam es oft vor, dass die Kinder mehr Gegenstände nahmen, als auf der Karte angegeben waren, und dies lag nicht immer daran, dass sie sich nicht an die Anzahl erinnerten, sondern entsprang einer Sucht nach möglichst vielen Gegenständen. Ein wenig von jener instinktiven Gier, die dem primitiven und unkultivierten Menschen gemeinsam ist. Die Direktorin versucht den Kindern zu erklären, dass es sinnlos ist, all diese Dinge auf dem Schreibtisch zu haben, und dass der Sinn des Spiels darin besteht, genau die Anzahl der benötigten Gegenstände zu nehmen.

Nach und nach kommen sie auf diese Idee, aber nicht so einfach, wie man annehmen könnte. Es ist eine echte Anstrengung der Selbstverleugnung, die das Kind innerhalb der gesetzten Grenzen hält und es beispielsweise dazu bringt, nur zwei der ihm zur Verfügung gestellten Gegenstände zu nehmen, während es sieht, wie andere mehr nehmen. Ich betrachte dieses Spiel daher eher als eine Übung der Willenskraft als des Zählens. Das Kind, das die Null hat , sollte sich nicht von seinem Platz bewegen, wenn es sieht, wie alle seine Gefährten aufstehen und sich frei von den Gegenständen nehmen, die ihm unzugänglich sind. Oftmals fällt die Null auf das Los eines Kindes, das perfekt zu zählen weiß und große Freude daran haben würde, eine schöne Gruppe von Gegenständen in der richtigen Reihenfolge auf seinem Tisch zu sammeln und anzuordnen und mit Sicherheit auf die Bestätigung des Lehrers zu warten.

Es ist sehr interessant, die Gesichtsausdrücke derjenigen zu studieren, die Null besitzen. Die daraus resultierenden individuellen Unterschiede sind geradezu eine Offenbarung des „Charakters“ eines jeden. Einige bleiben teilnahmslos und nehmen eine kühne Front an, um den Schmerz der Enttäuschung zu verbergen; andere zeigen diese Enttäuschung durch unfreiwillige Gesten. Wieder andere können das Lächeln nicht verbergen, das die einzigartige Situation, in der sie sich befinden, hervorruft und ihre Freunde neugierig macht. Es gibt Kleine, die jede Bewegung ihrer Gefährten mit sehnsüchtigem, fast neidischem Blick verfolgen, andere akzeptieren die Situation sofort. Nicht weniger interessant sind die Ausdrücke, mit denen sie sich zum Halten der Null bekennen, wenn sie während der Überprüfung gefragt werden: "Und Sie, Sie haben nichts genommen?" "Ich habe null." "Es ist null." Dies sind die üblichen Worte, aber das ausdrucksstarke Gesicht und der Ton der Stimme zeigen sehr unterschiedliche Gefühle. In der Tat gibt es selten diejenigen, die mit Vergnügen die Erklärung einer außergewöhnlichen Tatsache geben. Die größere Zahl sieht entweder unglücklich oder einfach nur resigniert aus.

Wir geben daher Lektionen über die Bedeutung des Spiels und sagen: "Es ist schwer, keine Geheimnisse zu bewahren. Falten Sie das Papier fest und lassen Sie es nicht wegrutschen. Es ist das Schwierigste von allen." In der Tat, nach einer Weile reizt die Schwierigkeit, still zu bleiben, die Kinder, und wenn sie den Zettel mit der Null öffnen, kann man sehen, dass sie zufrieden sind, das Geheimnis zu bewahren.

19.3 Addition und Subtraktion von eins bis zwanzig: Multiplikation und Division

Das didaktische Material, das wir für die Vermittlung der ersten Rechenoperationen verwenden, ist das gleiche, das bereits für das Numerieren verwendet wird; das heißt, die der Länge nach abgestuften Stäbe, die, auf der Skala des Meters angeordnet, die erste Idee des Dezimalsystems enthalten.

Die Stäbe werden, wie gesagt, nach den Zahlen benannt, die sie darstellen; eins, zwei, drei usw. Sie sind in der Reihenfolge der Länge angeordnet, die auch in der Reihenfolge der Nummerierung ist.

Die erste Übung besteht darin, die kürzeren Teile so zusammenzusetzen, dass Zehner entstehen. Der einfachste Weg, dies zu tun, besteht darin, nacheinander die kürzesten Stäbe von einem nach oben zu nehmen und sie am Ende der entsprechenden langen Stäbe von neun nach unten zu platzieren. Dies kann von den Befehlen begleitet werden: "Nimm eins und füge es zu neun hinzu; nimm zwei und füge es zu acht hinzu; nimm drei und füge es zu sieben hinzu; nimm vier und füge es zu sechs hinzu." Auf diese Weise machen wir vier Stangen gleich zehn. Es bleibt die Fünf, aber diese auf den Kopf gestellt (im langen Sinn), sie geht von einem Ende der Zehn zum anderen und macht so deutlich, dass zwei mal fünf zehn macht.

Diese Übungen werden wiederholt und dem Kind wird nach und nach die Fachsprache beigebracht; neun plus eins gleich zehn, acht plus zwei gleich zehn, sieben plus drei gleich zehn, sechs plus vier gleich zehn, und für die fünf, die übrig bleiben, zwei mal fünf gleich zehn. Endlich, wenn er schreiben kann, lehren wir die Zeichen plus und gleich und Zeiten. Dann sehen wir das in den hübschen Notizbüchern unserer Kleinen:

9+1=10
  
8+2=10
         5x2=10
7+3=10
  
6+4=10

Wenn dies alles gut erlernt ist und von den Kindern mit großer Freude zu Papier gebracht wurde, machen wir sie auf die Arbeit aufmerksam, die entsteht, wenn die zu Zehnern gruppierten Stücke auseinandergenommen und wieder an ihren ursprünglichen Platz gebracht werden. Von den zehn zuletzt Gebildeten nehmen wir vier und sechs Reste weg; vom nächsten nehmen wir drei und sieben Überreste weg; vom nächsten bleiben zwei und acht übrig; vom letzten nehmen wir einen und neun Überreste weg. Wenn wir richtig darüber sprechen, sagen wir, zehn weniger vier gleich sechs; zehn weniger drei gleich sieben; zehn weniger zwei gleich acht; zehn weniger eins gleich neun.

Was die verbleibenden fünf betrifft, so ist es die Hälfte von zehn, und wenn wir den langen Stab in zwei Teile schneiden, dh zehn durch zwei teilen, hätten wir fünf; zehn geteilt durch zwei ergibt fünf. Die schriftliche Aufzeichnung all dessen lautet:

Wenn die Kinder diese Übung beherrschen, multiplizieren sie sie spontan. Können wir drei auf zwei Arten machen? Wir setzen die Eins hinter die Zwei und schreiben dann, damit wir uns daran erinnern können, was wir getan haben, 2+1=3. Können wir zwei Stäbe gleich der Zahl vier machen? 3+1=4 und 4-3=1; 4-1=3. Stab Nummer zwei wird in seiner Beziehung zu Stab Nummer vier so behandelt, wie es fünf in Bezug auf zehn war; das heißt, wir drehen es um und zeigen, dass es genau zweimal in vier enthalten ist: 4/2=2; 2x2=4. Ein weiteres Problem: Lassen Sie uns sehen, mit wie vielen Stangen wir dasselbe Spiel spielen können. Wir können es mit drei und sechs und mit vier und acht machen; das ist,

2x2=4     3x2=6    4x2=8    5x2=10  
10/2=5    8/2=4    6/2=3    4/2=2

An dieser Stelle stellen wir fest, dass die Würfel, mit denen wir die Zahlen-Memory-Spiele gespielt haben, eine Hilfe sind:

Aus dieser Anordnung sieht man sofort, welche Zahlen durch zwei teilbar sind, all jene, die unten keinen ungeraden Würfel haben. Dies sind die geraden Zahlen, weil sie zu zweit paarweise angeordnet werden können; und die Division durch zwei ist einfach, man braucht nur die beiden untereinander stehenden Zweierlinien zu trennen. Wenn wir die Würfel jeder Datei zählen, haben wir den Quotienten. Um die primitive Zahl neu zusammenzusetzen, müssen wir nur die beiden Dateien neu zusammensetzen, also 2x3=6. All dies ist für Kinder von fünf Jahren nicht schwierig.

Die Wiederholung wird bald eintönig, aber man kann die Übungen am leichtesten ändern, indem man den Satz langer Stäbe wieder nimmt und den Stab Nummer eins nicht nach neun, sondern nach zehn legt. Platzieren Sie auf die gleiche Weise zwei nach neun und drei nach acht. Auf diese Weise machen wir Stäbe von größerer Länge als zehn; Längen, die wir elf, zwölf, dreizehn usw. bis hin zu zwanzig nennen lernen müssen. Auch die kleinen Würfel können verwendet werden, um diese höheren Zahlen festzulegen

Nachdem wir die Operationen bis zehn gelernt haben, gehen wir ohne Schwierigkeiten bis zwanzig weiter. Die eine Schwierigkeit liegt in den Dezimalzahlen, die bestimmte Lektionen erfordern.

19.4 Lektionen über Dezimalzahlen: arithmetische Berechnungen über zehn hinaus

Das notwendige didaktische Material besteht aus einer Anzahl quadratischer Karten, auf denen die Zahl zehn in großer Schrift gedruckt ist, und aus anderen rechteckigen Karten, die halb so groß sind wie das Quadrat und die einzelnen Zahlen von eins bis neun enthalten. Wir platzieren die Zahlen in einer Reihe; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Wenn wir dann keine Zahlen mehr haben, müssen wir wieder von vorne beginnen und wieder die 1 nehmen. Diese 1 ist wie der Abschnitt im Rutensatz, der bei Rute Nummer 10 über neun hinausgeht. Zählen entlang der Treppe bis neun bleibt dieser eine Abschnitt, den wir, da keine Zahlen mehr vorhanden sind, wieder mit 1 bezeichnen; aber dies ist eine höhere 1 als die erste, und um sie von der ersten zu unterscheiden, setzen wir daneben eine Null, ein Zeichen, das nichts bedeutet. Hier ist also die 10. Wenn wir die Null mit den einzelnen rechteckigen Zahlenkarten in der Reihenfolge ihrer Abfolge abdecken, sehen wir Folgendes gebildet: 11, 12, 13, 14, 15, 16, 17, 18, 19. Diese Zahlen werden durch Addieren zum Stab zusammengesetzt Nummer 10, zuerst Stange Nummer 1, dann 2, dann 3 usw., bis wir schließlich Stange Nummer 9 zu Stange Nummer 10 hinzufügen und so eine sehr lange Stange erhalten, die, wenn sie abwechselnd rote und blaue Abschnitte zählt, ergibt wir neunzehn.

Die Direktorin darf dann dem Kind die Karten mit der Zahl 16 zeigen, und es darf Stab 6 nach Stab 10 legen. Dann nimmt sie die Karte mit der 6 weg und legt über die Null die Karte mit der Ziffer 8, woraufhin das Kind entfernt Stab 6 und ersetzt ihn durch Stab 8, wodurch 18 entsteht. Jede dieser Handlungen kann folgendermaßen aufgezeichnet werden: 10 + 6 = 16; 10+8=18 usw. Bei der Subtraktion gehen wir genauso vor.

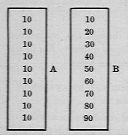
Wenn die Zahl selbst für das Kind eine klare Bedeutung zu haben beginnt, werden die Kombinationen auf einer langen Karte gemacht, wobei die rechteckigen Karten mit den neun Ziffern auf den zwei Zahlenreihen angeordnet werden, die in den Abbildungen A und B gezeigt werden.

Auf die Karte A legen wir die Null der zweiten 10, die rechteckige Karte mit der 1: und darunter die mit der Zwei usw. Während also eine der Zehn gleich bleibt, gehen die Zahlen rechts von Null bis Neun weiter, daher:

Bei Karte B sind die Anwendungen komplexer. Die Karten sind in Zehnerreihenfolge übereinandergelegt.

Fast alle unsere Kinder zählen bis 100, eine Zahl, die ihnen als Reaktion auf ihre Neugier beim Lernen gegeben wurde.

Ich glaube nicht, dass diese Phase des Unterrichts weiterer Erläuterungen bedarf. Jeder Lehrer kann die praktischen Übungen in den Rechenoperationen vervielfachen, indem er einfache Gegenstände verwendet, die die Kinder leicht handhaben und teilen können.

Die Lizenz dieser Seite:

Diese Seite ist Teil des „ Montessori Restoration and Translation Project “.
Bitte unterstützen Sie unsere Initiative „ All-Inclusive Montessori Education for All 0-100+ Worldwide “. Wir erstellen offene, kostenlose und erschwingliche Ressourcen für alle, die sich für Montessori-Pädagogik interessieren. Wir verwandeln Menschen und Umgebungen weltweit in authentische Montessori. Danke!

Lizenz: Dieses Werk mit all seinen Restaurierungsbearbeitungen und Übersetzungen ist unter einer Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License lizenziert .

Schauen Sie sich den Seitenverlauf jeder Wiki- Seite in der rechten Spalte an, um mehr über alle Mitwirkenden und Bearbeitungen, Wiederherstellungen und Übersetzungen zu erfahren, die auf dieser Seite vorgenommen wurden.

Beiträge und Sponsoren sind willkommen und werden sehr geschätzt!

Die Montessori-Methode, 2. Auflage - Deutsche Restaurierung - Archive.Org - Open Library

1912 - The Montessori Method

The Montessori Method by Maria Montessori - Montessori Translation Project